Jenis Bilangan Bulat dan Contoh Soal Bilangan Bulat Lengkap – Bilangan bulat sangat banyak jenisnya maka akan di jelaskan dan di jabarkan sebagai berikut.
Jenis Bilangan Bulat dan Contoh Soal Bilangan Bulat Lengkap
Berikut jenis dan contoh soal bilangan bulat.
Jenis Bilangan Bulat
Bilangan bulat trediri dari berbagai jenis bilangan seperti bilangan cacah (0, 1, 2, 3, 4, 5, … dst.) serta bilangan negatif (-1, -2, -3, -4, -5, … dst.. bilangan bulat bisa dituliskan tanpa ada komponen desimal atau pecahan.
Bilangan bulat merupakan himpunan. Himpunan sendiri berarti bahwa semua bilangan bulat dalam ilmu matematika dan dituliskan dengan lambang “Z” yang merupakan singkatan dari “Zahlen” dalam bahasa Jerman yang artinya bilangan.
Himpunan Z tertutup di bawah operasi perkalian dan penjumlahan. Hal itu berarti bahwa jumlah serta hasil kali antara dua bilangan bulat akan tetap berupa bilangan bulat.
Tetapi, berbeda dengan bilangan asli, himpunan Z pun tertutup di dalam operasi pengurangan tetapi tidak dengan pembagian. Hasil pembagian antara dua bilangan bulat belum tentu menghasilkan bilangan bulat pula.
Bilangan bulat dikategorikan sebagai bilangan rasional yang menjadi bagian dari bilangan real. Selain bilangan bulat negatif, bilangan lain yang termasuk ke dalam bilangan bulat adalah bilangan nol {0} dan bilangan asli (bilangan bulat positif) = {1, 2, 3, 4, 5, 6, … dst.). Bilangan asli pun dibagi lagi menjadi bilangan ganjil (1, 3, 5, 7, 9, … dst.) dan bilangan genap (2, 4, 6, 8, 10, … dst).
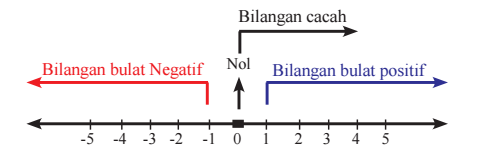
Bilangan nol dengan bilangan asli membentuk himpunan bilangan yang dinamakan bilangan cacah (0, 1 , 2, 3, 4, 5, 6, … dst). Perhatikanlah gambar di bawah ini tentang garis bilangan.
Mengurutkan Bilangan Bulat
Cara untuk mengurutkan bilangan bulat yakni dengan menuliskan bulat bulat secara runtut mulai dari nilai yang paling besar atau nilai terkecil. Dalam garis bilangan, makin ke kanan posisi suatu bilangan, maka nilainya akan makin membesar. Begitu juga jika makin kiri letak suatu bilangan, maka nilainya akan mengecil.
Membandingkan Bilangan Bulat
Ada lambang-lambang yang dipakai dalam perbandingan antara bilangan bulat yaitu :
- Apabila bilangan p lebih besar dari bilangan q, maka penulisannya p > Lambang (>) dibaca lebih besar dari.
- Apabila bilangan p lebih kecil dari bilangan q, maka penulisannya p < Lambang (<) dibaca lebih kecil dari atau kurang dari.
- Apabila bilangan p lebih dari atau sama dengan bilangan q, maka penulisannya p ³ Lambang (³) dibaca lebih besar atau sama dengan.
- Apabila bilangan p kurang dari atau sama dengan bilangan q, maka penulisannya p £ Lambang (£) dibaca kurang dari atau sama dengan.

Perlu diingat bahwa nilai nilangan positif akan selalu besar dibandingkan bilangan positif.
Invers (Lawan) Bilangan Bulat
Kebalikan atau invers (lawan) dari bilangan positif adalah bilangan negatif. Invers dari p adalah –p. Misalnya, invers dari -90 adalah 90 dan invers dari 35 adalah -35.
Contoh Soal Bilangan Bulat
Berikut ini adalah kumpulan bilangan cacah : 6.397.832, -983.765, 4.487.832 dan -928.372. Urutkanlah kumpulan bilangan tersebut mulai dari yang paling kecil!
Jawaban
Kumpulan bilangan tersebut tidak termasuk dalam bilangan cacah sebab terdapat dua bilangan bulat negatif yaitu -983.765 dan -928.372 serta tidak ada bilangan nol.
Jadi, yang termasuk dalam bilangan cacah hanya bilangan 6.397.832 dan 4.487.832. Kemudian, membandingkan dua bilangan tersebut dan diketahui bahwa 4.487.832 < 6.397.832. Kesimpulannya adalah 4.487.832 dan 6.397.832.
Berapakah hasil dari 21 : (3 – 10) + 4 x (-2)?
Jawaban
Dalam contoh soal seperti ini, kerjakanlah terlebih dulu operasi bilangan dalam kurung. Kemudian, kerjakan operasi kali dan bagi. Setelah itu, kerjakan operasi tambah dan kurang.
= 21 : (3 – 10) + 4 x (-2)
= 21 : (-7) + (-8)
= (-3) + (-8)
= -11
Jadi, hasil dari 21 : (3 – 10) + 4 x (-2) adalah -11.
Berapakah hasil dari 28 + 7 x (-5)?
Jawaban
Pengerjaan soal ini sama dengan soal sebelumnya.
= 28 +7 x (-5)
= 28 + (-35)
= -7
Jadi, hasil dari 28 + 7 x (-5) adalah -7.
Hitunglah hasil operasi dari (-12) + 20 x 4 – (-6) : 3!
Jawaban
= (-12) + 20 x 4 – (-6) : 3
= (-12) + 80 – (-2)
= (-12) + 80 + 2
= (-12) + 82
= 70
Jadi, hasil dari (-12) + 20 x 4 – (-6) : 3 adalah 70.
Berapakah hasil dari 14 + (18 : (-3)) – ((-2) x 3)?
Jawaban
= 14 + (18 : (-3)) – ((-2) x 3)
= 14 + (-6) – (-6)
= 14 – 6 + 6
= 14 – 0
= 14
Jadi, hasil dari 14 + (18 : (-3)) – ((-2) x 3) adalah 14.
Berapakah nilai q yang memenuhi (12 + 8) + (-3q) = -22
Jawaban
(12 + 8) + (-3q) = -22
20 + (-3q) = -22
20 + 22 = 3q
42 = 3q
42 : 3 = 3q : 3
14 = 4
Jadi, nilai q yang memenuhi (12 + 8) + (-3q) = -22 adalah 14.
Berapakah hasil dari 72 – (520 : 8) ?
Jawaban
= 72 – (520 : 8)
= 72 – 65
= 7
Jadi, hasil dari 72 – (520 : 8) adalah 7.
Suhu awal sebuah ruangan yakni 27 o ruangan itu dipakai menyimpan ikan dan suhunya menjadi -3 oC. Berapakah perubahan suhu yang terjadi dalam ruangan tersebut?
Jawaban
= 27 – (-3)
= 27 + 3
= 30
Jadi, perubahan suhu yang terjadi dalam ruangan tersebut adalah 30 oC.
Itulah penjelasan materi Jenis Bilangan Bulat dan Contoh Soal Bilangan Bulat Lengkap. Semoga penjelasan materi yang diserta contoh dan pembahasan tersebut bisa menambah pemahaman para pembaca. Terima kasih 🙂